我们正在玩一个猜数游戏，游戏规则如下：

1. 我从 1 到 n 之间选择一个数字。
2. 你来猜我选了哪个数字。
3. 如果你猜到正确的数字，就会 赢得游戏 。
4. 如果你猜错了，那么我会告诉你，我选的数字比你的 更大或者更小 ，并且你需要继续猜数。
5. 每当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。如果你花光了钱，就会 输掉游戏 。

给你一个特定的数字 n ，返回能够 确保你获胜 的最小现金数，不管我选择那个数字 。

示例 1：

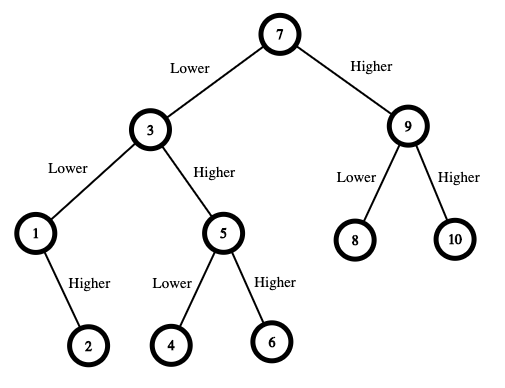
输入：n = 10
输出：16
解释：制胜策略如下：
- 数字范围是 [1,10] 。你先猜测数字为 7 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $7 。
    - 如果我的数字更大，则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $9 。
        - 如果我的数字更大，那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏，总费用为 $7 + $9 = $16 。
        - 如果我的数字更小，那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏，总费用为 $7 + $9 = $16 。
    - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $3 。
        - 如果我的数字更大，则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $5 。
            - 如果我的数字更大，那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
            - 如果我的数字更小，那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
        - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $1 。
            - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $7 + $3 + $1 = $11 。
在最糟糕的情况下，你需要支付 $16 。因此，你只需要 $16 就可以确保自己赢得游戏。

示例 2：

输入：n = 1
输出：0
解释：只有一个可能的数字，所以你可以直接猜 1 并赢得游戏，无需支付任何费用。

示例 3：

输入：n = 2
输出：1
解释：有两个可能的数字 1 和 2 。
- 你可以先猜 1 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $1 。
    - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $1 。
最糟糕的情况下，你需要支付 $1 。

提示：

• 1 <= n <= 200