分享｜前缀和刷题笔记

2021.11.17

发布于重庆

前缀和分享技术交流

前言

前缀和和差分数组都是数组算法中常见的算法思想，都是通过预处理建立数组进行操作，并且两者非常相似，本文记录学习两者的一些笔记。

说明

什么是前缀和数组？

前缀和数组是指对原数组进去前缀和运算得到的新数组。即 presum[i]=nums[0]+..+nusm[i-1].

什么是差分数组？

差分数组是指对原数组进行差分运算得到的新数组，即 diffix[i]=nums[i]-nums[i-1].

两种构建通过提前预处理构建新数组，在一些区间操作中可以优化复杂度。

前缀和与差分数组的转换关系如下：

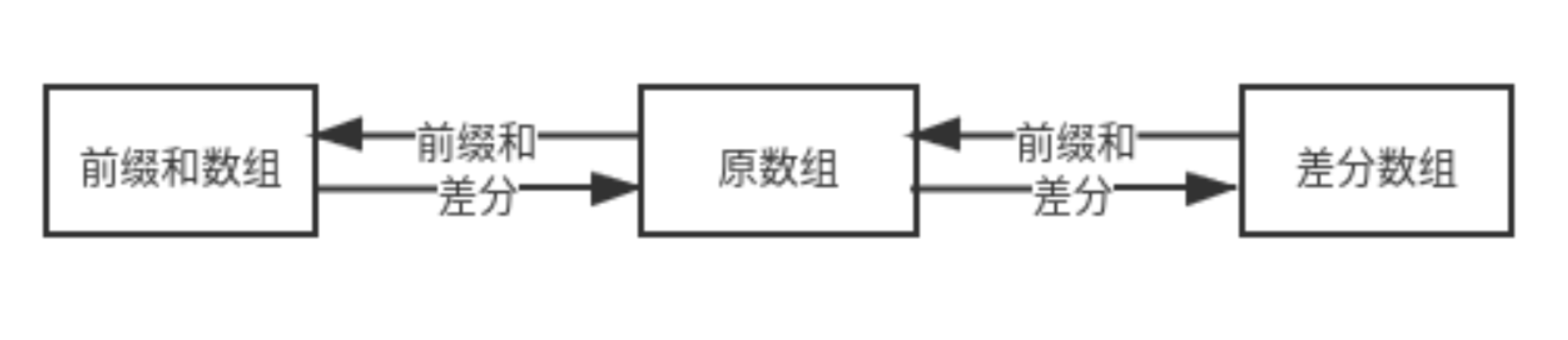
通常来说，假设原数组为 nums，前缀和数组为 prefix，差分数组为 diffix。那么 nums 和 diffix 的长度相等，而 prefix 要多一个元素，插入第一个元素为 0，二维则是左侧和上方多一排元素，这可以方便代码编写。

通常来说，有这些操作：

对原数组求前缀和数组（可以在原数组基础上做）
对原数组求差分数组
对前缀和数组查询任意区间的和
差分数组修改任意区间
差分数组求原数组

模板

前缀和

新开数组

class prefixSum {
private:
    vector<int> presum;

public:
    prefixSum(const vector<int> &nums) {
        presum.resize(nums.size() + 1);
        presum[0] = 0;
        for (int i = 1; i < presum.size(); i++) {
            presum[i] = presum[i - 1] + nums[i - 1];
        }
    }

		// 求 [i,j] 区间的和
    int sumRange(int i, int j) {
        return presum[j + 1] - presum[i];
    }

    int num(int i) {
        return sumRange(i, i + 1);
    }
};

在原数组的基础上

class NumArray {
public:
    NumArray(vector<int>& nums) {
				nums.insert(nums.begin(),0);
				for (int i=1;i<nums.size();i++){
            nums[i]+=nums[i-1];
        }
    }
};

差分数组

新数组

class diffSum {
private:
    vector<int> diffsum;

public:
    diffSum(vector<int> nums) {
        diffsum.resize(nums.size());
        diffsum[0] = nums[0];

        for (int i = 1; i < nums.size(); ++i) {
            diffsum[i] = nums[i] - nums[i - 1];
        }
    }

    void show() {
        for (int i : diffsum) {
            cout << i << endl;
        }
    }

    void op(int l, int r, int val) {
        diffsum[l] += val;
				if (r+1<diffsum.size() {
		        diffsum[r + 1] -= val;
				}
    }

    vector<int> originArr() {
        vector<int> res(diffsum.size());
        res[0] = diffsum[0];
        for (int i = 1; i < res.size(); i++) {
            res[i] = res[i - 1] + diffsum[i];
        }

        for (const auto &item : res) {
            cout << item << endl;
        }

        return res;
    }
};

二维前缀和

class NumMatrix {
private:
    vector<vector<int>> presum;

public:
    NumMatrix(vector<vector<int>>& matrix) {
        presum.resize(matrix.size()+1,vector<int>(matrix[0].size()+1));
        for (int i=1;i<=matrix.size();i++){
            for (int j=1;j<=matrix[0].size();j++){
                presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+matrix[i-1][j-1];
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        row1++;
        col1++;
        row2++;
        col2++;

        return presum[row2][col2]-presum[row2][col1-1]-presum[row1-1][col2]+presum[row1-1][col1-1];
    }
};

应用

前缀和与差分都是用在区间操作中的，同样的数据结构还有树状数组，线段树等等。

而前缀和与差分的区别在于：

前缀和主要用于原数组不会变化的情况下，频繁查询区间和
差分则是用于频繁对原数组某区间元素进行增删的时候

上面是前缀和与差分的基本运算，实际上还有一些引申，比如前缀和可能不是求和，而是求前缀数组的某个性质，比如说字符种类等等。也可能是异或，乘积运算，而不是和。

除了前缀外，也可能与后缀和同时使用等。

而前缀和通常是求两个 presum，是确定的，暴力就是遍历两遍 $O (n^{2})$ ，而常见的优化方式就是用哈希表存储左边的 presum，遍历右边的 presum，优化到线性。

同时，在计数问题中，比如 xx 出现多少次，xx 和 xx 的数量相等这种问题，经常可以把原数组进行变化，如变化为相反数 1 和 -1，或者 0，把计数问题转换为求和问题。

此外，前缀和还经常和同余定理同时使用，同余定理：
(presum2-presum1)%k → presum2%k-presum1%k=0 → (presum2%k+k)%k=(presum1%k+k)%k.

题目

基础前缀和

一些原始前缀和使用题型，练习模板和基础思路

list

303. 区域和检索 - 数组不可变

求区间 [i,j] 的和，如果用高中数列的实现来思考，即 $a_{i} + a_{i + 1} + ... + a_{j}$ .

而

$s u m_{i - 1} = a_{0} + a_{1} + ... a_{i - 1} s u m_{j} = a_{0} + a_{1} + ... + a_{i - 1} + a_{i} + a_{i + 1} + ... a_{j} = s u m_{i - 1} + a_{i} + a_{i + 1} + ... + a_{j} 显然 a_{i} + a_{i + 1} + ... + a_{j} = s u m_{j} - s u m_{i - 1}$

也就是说，如果要求得某个区间的和，如果能提前知道两边界的数组和，那么是很容易求解的。自然的，我们就可以提前把这些数组和给提前求出来，这些和组成的数组就被称为前缀和数组。

对于前缀和数组 presum,有

$p res u m [i] = n u m s [0] + n u m s [1] + .. n u m s [i - 1]$

成立，也就是说，presum[i] 的值是 nums[i] 元素前面所有元素的和。

如

无效的图片地址

我们需要注意两点：

nums[0] 前后没有元素，所以设 presum[0]=0

计算如下：

无效的图片地址

但是我们发现 nums[5] 是最后一个元素，它有前面的所有元素，但是 nums[5] 本身缺没有计算进去，因为后面没有元素，自然不能计算在 前面所有元素里 了。所以，我们需要在前缀和数组后面再加一个元素，值就是原数组所有元素之和。

无效的图片地址

自然的，我们可以发现，前缀和数组要比原数组个数要多一个。

那么 presum 数组应该怎么构造呢？我们知道

$p res u m [i] = s u m_{i - 1} p res u m [i - 1] = s u m_{i - 2} p res u m [i] = p res u m [i - 1] + s u m_{i - 1} - s u m_{i - 2} = p res u m [i - 1] + n u m s [i - 1]$

即 $p res u m [i] = p res u m [i - 1] + n u m s [i - 1]$ ，注意 i≥1，当 i=1 时，presum[i]=0

现在我们已经构造出前缀和数组了，那么我们怎么计算 $[i, j]$ 区间的和呢？

$前面说过 : a_{i} + a_{i + 1} + ... + a_{j} = s u m_{j} - s u m_{i - 1} p res u m [i] = s u m_{i - 1} 故： res = p res u m [j + 1] - s u m [i]$

代码如下:

class NumArray {
public:
    vector<int> presum;

    NumArray(vector<int>& nums) {
        presum.resize(nums.size()+1);

        presum[0]=0;

        for (int i=1;i<presum.size();i++){
            presum[i]=presum[i-1]+nums[i-1];
        }
    }
    
    int sumRange(int left, int right) {
        return presum[right+1]-presum[left];
    }
};

前面我们知道，前缀和数组虽然比原数组多一个元素，但是第一个元素永远都是 0，因此我们实际上可以直接在修改原数组得到前缀和数组，优化如下

class NumArray {
public:
    vector<int> *p;

    NumArray(vector<int>& nums) {
        for (int i=1;i<nums.size();i++){
            nums[i]=nums[i]+nums[i-1];
        }
        p=&nums;
    }
    
    int sumRange(int left, int right) {
        if (left==0){
            return p->at(right);
        } 
        return p->at(right)-p->at(left-1);
    }
};

1480. 一维数组的动态和

just ac

class Solution {
public:
    vector<int> runningSum(vector<int>& nums) {        
        for (int i=1;i<nums.size();i++){
            nums[i]+=nums[i-1];
        }
        return nums;
    }
};

1991. 找到数组的中间位置

一看题目，求左子数组和右子数组的和相等，数组没有发生变化，求子数组的和，自然想到使用前缀和数组。

我们知道求 [l,r] 区间的和等于 presum[r+1]-presum[l]，而本题假设目标索引是 i，则有 presum[0,i-1]==presum[i+1,presum.size()-1]，故我们遍历 i 然后判断即可。

class Solution {
public:
    int pivotIndex(vector<int>& nums) {
        // 构造前缀和数组
        vector<int> presum(nums.size()+1);
        presum[0]=0;
        for (int i=1;i<presum.size();i++){
            presum[i]=presum[i-1]+nums[i-1];
        }

        for (int i=0;i<presum.size()-1;i++){
            // [0,i-1] 区间的和等于 [i+1,presum.size()-1]
            if ((presum[i]-presum[0])==(presum[presum.size()-1]-presum[i+1])){
                return i;
            }
        }

        return -1;
    }
};

643. 子数组最大平均数 I

本题求连续子数组，故第一反应就应该想到滑动窗口，而这题求平均数最大，数的个数又最大，也就是说，窗口 k 里的和最大，使用滑动窗口很容易求解。不过这题数组又没有变化，又涉及到子数组求和，那么自然也可以想到前缀和数组。

也就是说，求 [i,i+k-1] 区间和的最大值，那么直接对 i 遍历求 presum[i+k]-presum[i] 的最大值即可。

class Solution {
public:
    double findMaxAverage(vector<int>& nums, int k) {
        vector<int> presum(nums.size()+1);
        presum[0]=0;
        for(int i=1;i<presum.size();i++){
            presum[i]=presum[i-1]+nums[i-1];
        }

        int sum=-9999999999;

        for(int i=0;i<presum.size()-k;i++){
            if (presum[i+k]-presum[i] > sum){
                sum=presum[i+k]-presum[i];
            }
        }

        return (double)sum/k;
    }
};

1413. 逐步求和得到正数的最小值

本题的意思就是，选定一个初始值，然后遍历 nums 数组加到和中去，那么自然值就等于当前 i 的前缀和+初始值，而要使得最终和大于等于 1，即 presum[i]+startvalue≥1，要找 startvalue 的最小值，故只需 min(presum[i])+min(startvalue)=1,即求 presum 的最小值即可。

class Solution {
public:
    int minStartValue(vector<int>& nums) {
        int i=1;
        int min=nums[0];

        for (;i<nums.size();i++){
            nums[i]=nums[i]+nums[i-1];
        }

        for (i=0;i<nums.size();i++){
            if (min > nums[i]){
                min=nums[i];
            }
        }

        if (min >= 1){
            return 1;
        }

        return 1-min;
    }
};

1588. 所有奇数长度子数组的和

求所有奇数子数组的和，且原数组没有修改，又求连续子数组的和，自然想到前缀和。

假设某个奇数子数组以 i 索引开头，那么应该有 [i,i],[i,i+2],[i,i+4]...，[i,i+2k]，且 2k ≤ nums.size()

那么我们可以遍历 i 然后求和

class Solution {
public:
    int sumOddLengthSubarrays(vector<int>& arr) {
        int res=0;
        vector<int> presum(arr.size()+1);
        presum[0]=0;
        for (int i=1;i<presum.size();i++){
            presum[i]=presum[i-1]+arr[i-1];
        }

        // [i,i+2k]
        for (int i =0;i<presum.size();i++) {
            for (int k = 0;i+2*k+1 < presum.size();k++) {
                res += (presum[2*k+i+1]-presum[i]);
            }
        }

        return res;
    }
};

1732. 找到最高海拔

对差分数组求原数组，并且求最大值。

class Solution {
public:
    int largestAltitude(vector<int>& gain) {
        vector<int> arr(gain.size()+1);
        arr[0]=0;

        for (int i=1;i<arr.size();i++){
            arr[i]=arr[i-1]+gain[i-1];
        }

        int max=arr[0];
        for (int i=0;i<arr.size();i++){
            if (max<arr[i]){
                max=arr[i];
            }
        }
        return max;
    }
};

优化，在原数组的基础上求解，注意原数组比差分数组多一个元素，故第一个元素 0 漏掉了，还要比较下。

class Solution {
public:
    int largestAltitude(vector<int>& gain) {
        int max=gain[0];

        for (int i=1;i<gain.size();i++){
            gain[i]+=gain[i-1];            
            if (max<gain[i]){
                max=gain[i];
            }
        }
        return max>0?max:0;
    }
};

哈希表优化

通常构造前缀和，然后判断区间和时，需要两个前缀和做差。那么自然的想法就是先构建前缀和，然后遍历两次前缀和，这时复杂度为 $O (n^{2})$ ，但通常我们都是确定一个前缀和后，另一个前缀和是满足一定条件的，我们只需要判断是否存在就行，而存在性判断问题，使用 hash 表可以很快解决。因此，通常前缀和使用哈希表进行优化，在构建前缀和时同时构建哈希表，然后通过哈希表和当前前缀和的值进行判断，只需遍历一次就能解决，降到 $O (n)$ .

问题是哈希表该存什么元素，这个要看具体前缀和求什么。

存的就是前缀和的元素，及其对应的索引。所以重点是前缀和求得是什么，一般是差值或者

hash 表存什么

求个数就存个数求长度就存下标

list

560. 和为 K 的子数组

题意

求和为 k 的子数组个数

分析

数组未修改，又频繁查询数组和，典型的前缀和使用场景。构造前缀和 O(n),然后遍历所有区间判断，遍历区间 O(n^2).

但是本题 1 <= nums.length <= 2 * 10^4 数量级 10^4，O(n^2) 显然会超时，故考虑优化。

暴力查询区间时，我们假设当前区间和为 m，又遍历区间判断是否存在和为 k-m 的区间，就是这个再次遍历的过程复杂度太高。但是实际上，我们根本没有必要遍历，像这种判断是否存在的应用场景，我们可以引入一个 hash 表来判断。

于是，可以在构建前缀和数组时，同时把和存在 hash 表中，然后再遍历前缀和，对于每个区间和，再判断和为 k-m 的区间有多少个，这就是和为 k 的子数组个数了。

这样构建前缀和与查询遍历的时间复杂度为 O(n),空间复杂度也为 O(n).

代码
```
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int,int> m;
        int cnt=0;
        nums.insert(nums.begin(),0);

        m[nums[0]]++;
        for (int i = 1;i<nums.size();i++) {            
            nums[i]+=nums[i-1];
            cnt+=m[nums[i]-k];
            m[nums[i]]++;           
        }

        return cnt;
    }
};
```
1248. 统计「优美子数组」

题意

求刚好有 k 个奇数的子数组个数。

分析

这题其实是 560 的一个进阶，560 求和为 k，而这题求有 k 个奇数，我们可以对原数组进行简单的变化，就能转换为 560 题。

既然 k 个奇数要转换为和为 k，那么我们可以把原数组偶数变为 0，奇数变为 1，那么当有 k 个奇数时，就满足和为 k 了。

代码
```
class Solution {
public:
    int numberOfSubarrays(vector<int>& nums, int k) {
        int cnt=0;
        unordered_map<int,int> m;
        nums.insert(nums.begin(),0);

				// 预处理
        for (int i=0;i<nums.size();i++){
            if (nums[i]%2==0){
                nums[i]=0;
            }else {
                nums[i]=1;
            }
        }

				// 计算
        m[nums[0]]++;
        for (int i=1;i<nums.size();i++){
            nums[i]+=nums[i-1];
            m[nums[i]]++;
            cnt+=m[nums[i]-k];
        }

        return cnt;
    }
};
```
优化

观察代码发现其实没必要预处理和遍历分开，可以一次遍历同时执行
```
class Solution {
public:
    int numberOfSubarrays(vector<int>& nums, int k) {
        int cnt=0;
        unordered_map<int,int> m;
        nums.insert(nums.begin(),0);

        m[0]++;
        for (int i=1;i<nums.size();i++){
            if (nums[i]%2==0){
                nums[i]=0;
            }else {
                nums[i]=1;
            }            
            nums[i]+=nums[i-1];
            m[nums[i]]++;
            cnt+=m[nums[i]-k];
        }

        return cnt;
    }
};
```
525. 连续数组

题意

求 0 和 1 个数相同的子数组个数。

分析

涉及到计数问题，通常可以转换为求和问题，这题也是一样，问题在于，怎么转换呢？如果能够转换为求和问题，那么这题就能够使用前缀和进行优化。

假设 0 的个数为 k，1 的个数也为 k，那么 0 的总分为 0，1 的总和为 k，数组的和也为 k。虽然转换成了求数组和为 k 的问题，但是 k 并不是一个固定的数，还是不方便使用前缀和。那么有什么办法，能让数组的和等于一个固定的值，使得其表示 0 和 1 的个数相等吗？

两数个数相等，又要和为固定值，那么自然的，似乎也只有两数为相反数的是否才满足了。假设 0 变成 1 的相反数 -1，那么当总数组长度为 2k 时，-1 的个数为 k，和为 -k，1 的个数为 k，和为 k，总数组和为 0.

那么，显然当 -1 和 1 个数相等时，其数组和为 0.现在问题就转换为，求子数组和为 0 的长度的最大值。这就转换为 560，1248 这种我们熟悉的题目了。

算法

现在我们再来根据分析给出处理步骤：
1. 把原数组 0 变成 -1
2. 求前缀和数组 presum
3. 遍历 presum 求区间和为 0 的数组，并更新 max 长度
优化

我们可以进行一些常见的优化
1. 在原有数组基础上求前缀和，降低空间复杂度
2. 更新 0 为 -1 和求前缀和时，可以一次遍历完成
3. 使用 hash 表存满足条件的 presum，防止暴力收缩降低空间复杂度
问题在于第三个优化，满足条件的 presum 具体需要满足什么条件？

我们来看，我们需要求的是什么：

和为 0 的子数组

我们直到区间和 sum=presum[i]-presum[j]，i 和 j 是子数组的两端点。换句话说，当 presum 数组中两个值相等时，它们中间的元素构成的区间和为 0.

而我们需要求的是什么？

和为 0 的子数组长度的最大值。

也就是说，假设两端点值为 m，那么我们需要知道两个 k 距离的最远值。自然的，值等于第一次出现 k 的位置和最后一次出现 k 位置的差。

现在我们先假设构造好了 hash 表和前缀和数组，我们要遍历求值，显然我们通常都是这么求的：

固定第一次出现的 k，然后求最后出现的 k。

也就是用双指针，前指针指向第一次，后指针查询。但实际上我们没有必要这么做，我们可以用 hash 表来存储第一次 k 出现的位置，然后遍历求最后出现的位置。

上面这个步骤显然只需要扫描一次 presum 即可，因为第一次出现肯定在之后出现位置的左边。而这个扫描过程其实可以和构建 presum 时一起完成。

现在我们再来总结一下过程：

扫描原数组，同时做这些事：
1. 更改当前数组的值，0 变成 -1
2. 构造当前元素的前缀和
3. 如果当前元素是第一次出现，存到 hash 表中
4. 如果不是第一次出现，那么更新数组长度
代码
```
class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        unordered_map<int,int> m;
        int max=0;
        nums.insert(nums.begin(),0);
        m[0]=0;
        for (int i=1;i<nums.size();i++){
            if (nums[i]==0){
                nums[i]=-1;
            }
            nums[i]+=nums[i-1];
            
            if (m.count(nums[i])){
                max=max>(i-m[nums[i]])?max:(i-m[nums[i]]);
            } else{
                m[nums[i]]=i;
            }
        }  

        return max;
    }
};
```
1124. 表现良好的最长时间段

题意

要求一个子数组，其中大于 8 的数字比小于 8 的数字多。

分析

既然题目中和具体数字无关，自与似乎大于 8 相关，那么我们可以简化一下题目，把大于 8 的数看做 1，小于 8 的看做 0.那么题目就变成，求子数组中，1 的个数比 0 的个数多。

而这个题目就与 525 类似，525 求的是 1 和 0 的个数相等，而这题 1 的个数比 0 的个数多。

那以 525 的思路为例，我们将大于 8 的数字变成 1，小于 8 的变成 -1，那么，这个题就变成求和大于 0 的最长子数组。

而涉及到未修改数组的区间查询，前缀和是个很好的工具。因此，我们可以构造前缀和数组 presum，那么问题就转换为，求 presum 数组中区间大于 0 的最长长度。

那么我们可以直接暴力 $O (n^{2})$ 查询，但是本题数量级 10^4，显然要超时，我们需要考虑怎么优化一下。

优化

在 525 中，由于求的是和等于 0 的情况，即 presum2-prsum1=0，那么对于 presum1,presum2 的值就是确定的，我们只需要判断 presum2 是否存在即可，而这种存在性问题使用哈希表非常快捷，于是我们使用哈希表预存了 presum 数组进行判断。

但是这题求的是 presum2-presum1>0，对于确定的 presum1,presum2 是一个范围的值，于是不好使用哈希表进行存储了，那我们该怎么做才好呢？

我们假设 presum2-presum1=k，来看 k 应该满足怎样的性质。由于原数组只有 -1 和 1，故 presum 元素间差值应该为 1.也就是说，k 的最小值应该是 1.

我们假设 k = 2，假设当前区间为 [l,r]，那么：
1. 若 presum[l-1]=-1，那么区间显然可以像左扩展，这是区间和为 3.
2. 若 presum[l-1]=1，假设区间和也向左扩张，那么区间为为 1.
也就是说，如果 presum2-presum1=2，那么无论左侧元素是什么，继续像左都是符合条件的。故，必然有 presum2-presum1=1。

也就是说，对于一个 presum2,那么满足条件的 presum1 必然是一个确定的数，我们只需要判断该数存在与否即可。这又变成了一个存在性问题，所以我们仍然可以使用哈希表来优化。

同时，由于要求 presum2-prsum1 > 0，当我们向右遍历 presum 数组时，如果 presum2 已经大于 0，我们可以直接更新答案。只有当 presum2 < 0 时，我们才需要寻找更小的 presum1.

代码

暴力
```
class Solution {
public:
    int longestWPI(vector<int>& hours) {
        int max=0;

        hours.insert(hours.begin(),0);

        for (int i=1;i<hours.size();i++){
            if (hours[i]>8) {
                hours[i]=1;
            } else {
                hours[i]=-1;
            }
            hours[i]+=hours[i-1];
        }

        for (int i=0;i<hours.size();i++){
            for (int j=i;j<hours.size();j++){
                if (hours[j]>hours[i]){
                    max=max>(j-i)?max:(j-i);
                }            
            }
        }

        return max;
    }
};
```
hash 表优化
```
class Solution {
public:
    int longestWPI(vector<int>& hours) {
        int max=0;
        unordered_map<int,int> m;
        hours.insert(hours.begin(),0);
        for (int i=1;i<hours.size();i++){
            hours[i] = hours[i]>8?1:-1;
            hours[i]+=hours[i-1]; 
            if (hours[i]>0){
                max=i;
            } else {
                if (m.count(hours[i])==0){
                    m[hours[i]]=i;
                }
                if (m.count(hours[i]-1)>0 && max < (i-m[hours[i]-1])){
                    max=i-m[hours[i]-1];
                }
            }
        }

        return max;
    }
};
```
面试题 17.05. 字母与数字

题意

求字母和数字个数相同的区间最大长度。

分析

参考 525 和 1124，这题也是一样的，求两类元素的个数问题，和具体的字符无关，1所以可以压缩为 0 和 1 两个字符，不过又要个数相同，即 cnt1=cnt2，那么 cnt1-cnt2=0，我们可以把个数问题转换为求和问题，只需转换为两个相反数，如 1 或 -1，那么个数相等时，区间和就为 0，故这个题就等价于：求区间和为 0 的最长长度。

故我们构造前缀和数组，然后暴力遍历两次即可。

优化

和一般的前缀和优化差不多，这题也是一个 presum[i]=presum[j] 存在性问题，故我们引入哈希表，存当前坐标 i 前的元素，只需两元素相等，那么就是我们要求的区间。

注意注意一个坑，这题数字不只是 0~9，有大于 10 的，字母也不都是大写字母，只给测试用例，也没给范围，坑爹。

效率

时间复杂度： $O (n)$

空间复杂度： $O (n)$

代码
```
class Solution {
public:
    vector<string> findLongestSubarray(vector<string>& array) {
        vector<int> prefix(array.size()+1);
        vector<int> arr(array.size());
        unordered_map<int,int> m;
        int length=0;
        int l=0;
        int r=0;

        for (int i=0;i<array.size();i++){
            if (((array[i][0]>='A') && (array[i][0]<='Z'))||((array[i][0]>='a') && (array[i][0]<='z'))){
                arr[i]=1;
            } else {
                arr[i]=-1;
            }
        }

        m[0]=0;
        for (int i=1;i<prefix.size();i++){
            prefix[i]=prefix[i-1]+arr[i-1];
            if (m.count(prefix[i])==0) {
                m[prefix[i]]=i;
                continue;
            }

            if (length<(i-m[prefix[i]])){
                length=i-m[prefix[i]];
                l=m[prefix[i]];
                r=i;
            } 
        }

        vector<string> res(array.begin()+l,array.begin()+r);        
        return res;
    }
};
```
974. 和可被 K 整除的子数组

题意

求和能被 k 整除的子数组。

分析

设计未修改数组的频繁区间查询，显然需要使用前缀和进行处理。故构建 presum 数组。

要使得和能被 k 整除，显然只需 (presum2-presum1)%k=0 即可。那么暴力遍历判断 O(n^2) 即可。

优化

但是本题数量级在 10^4 级别，O(n^2) 显然会超时，故考虑优化。

我们知道，对于 presum2，我们需要找一个 presum1 使得 (presum2-presum1)%k=0，显然这是一个存在性的问题，而设计到前缀和+存在性问题，我们通常可以使用哈希表来进行优化。

和 sum 能被 k 整除，即 sum%k=0，又 sum=persum2-presum1.故

(presum2-presum1)%k=0.根据同余定理，presum2%k=presum1%k.

但由于 presum2 可能为负数，故对其变化为 presum2%k=(presum2%k+k)%k，则有 (presum2%k+k)%k=(presum1%k+k)%k.

故对于 presum2，我们只需要找到 presum1，使得 (presum2%k+k)%k=(presum1%k+k)%k 满足即可。

则可以进行如下步骤：
1. 遍历 nums 数组
2. 对 nums[i] 构建前缀和
3. 对于 presum[i]，判断 (presum[i]%k+k)%k 存在的个数并计算
4. 将 (presum[i]%k+k)%k 存入哈希表中
代码

暴力
```
class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        int cnt=0;

        nums.insert(nums.begin(),0);
        for (int i=1;i<nums.size();i++){
            nums[i]+=nums[i-1];
        }

        for (int i=0;i<nums.size();i++){
            for (int j=i+1;j<nums.size();j++){
                if ((nums[j]-nums[i])%k==0){
                    cnt++;
                }
            }
        }

        return cnt;
    }
};
```
优化
```
class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        int cnt=0;
        int t;
        unordered_map<int,int> m;

        nums.insert(nums.begin(),0);
        m[0]++;
        for (int i=1;i<nums.size();i++){
            nums[i]+=nums[i-1];
            t=(nums[i]%k+k)%k;
            cnt+=m[t];
            m[t]++;
        }

        return cnt;
    }
};
```
523. 连续的子数组和

题意

求和为 k 的倍数，求长度至少为 2 的子数组。

分析

这题和 974 差不多，而且还要简单点，这题没有负数，而且只是求是否存在，而 974 有负数，求满足的个数。

类似于 974，构建前缀和数组 presum，就是求 (presum2-presum1)%k=0，由于没有负数，根据同余定理，就是求 presum2%k=presum1%k.

也就是说，对于一个 presum2，只要其它 presum%k 相等就满足。

这是很典型的存在问题，我们可以使用哈希表来存当前 presum 前面的 presum%k 的结果，如果当前 presum2%k 存在，那么说明前面存在 presum1 使得 presum2%k=presum1%k.

如果不限制区间长度的话，哈希表的 value 存 bool 即可，但是这里限制长度至少为 2，所以我们还需要限制长度。只要最长的长度比 2 大，那么就满足。

而求满足区间的最长长度，和 325，525 的做法差不多，哈希表的 value 存第一次出现的索引即可，之后满足的索引再相减，就能从最短的长度依次增加到最长长度。

代码
```
class Solution {
public:
    bool checkSubarraySum(vector<int>& nums, int k) {
        nums.insert(nums.begin(),0);
        unordered_map<int,int> m;

        m[0]=0;
        for (int i=1;i<nums.size();i++){
            nums[i]+=nums[i-1]; // 构造前缀和
            
            if (m.count(nums[i]%k)>0) { // 如果存在
                if (i-m[nums[i]%k]>1){ // 判断长度
                    return true;
                }
            } else {
                m[nums[i]%k]=i; // 不存在则放到哈希表中
            }            
        }

        return false;
    }
};
```
1524. 和为奇数的子数组数目

题意

求和为奇数的子数组

分析

求和为奇数，涉及***改数组的批量查询，故构造前缀和数组 presum。

求和为奇数，即 sum=(presum2-presum1)%2≠0.

暴力遍历前缀和数组 O(n^2) 即可。

优化

本题数量级在 10^5，显然暴力会超时，则考虑优化。

和一般前缀和数组类似，本题也是涉及到存在性问题，即对于 presum2,判断 presum1 的存在，而且是固定的值。那么自然就引入哈希表。

问题在于哈希表存些什么。

由于要使得 presum2-presum1 为奇数，那么自然的，只有两种情况，即奇数-偶数，或者偶数-奇数才行。

也就是说，presum 具体值是多少我们根本不在意，那么，我们可以考虑将其简化为两种状态，奇数为 1，偶数为 0.依次构造新的前缀和数组。

现在问题就转换为，假设 presum2=0，那么需要找到 presum1=1 的个数，或者 persum1=1，找 presum2=0 的个数。

而这自然的，便引入哈希表存 0 和 1 的个数。

那么，我们就只需遍历 presum 数组，然后根据当前的值，查询另一个值的个数，再计算即可。

代码
```
class Solution {
public:
    int numOfSubarrays(vector<int>& arr) {
        arr.insert(arr.begin(),0);
        unordered_map<int,int> m;
        int cnt=0;

        m[0]++;
        for (int i=1;i<arr.size();i++){
            arr[i]+=arr[i-1];
            arr[i]=arr[i]%2==0?0:1; // 构造奇偶前缀和数组
            if (arr[i]==0){ // 根据当前数，查找前方另一数的个数
                cnt+=m[1];
                cnt%=1000000007;
            } else {
                cnt+=m[0];
                cnt%=1000000007;
            }            
            m[arr[i]]++;            
        }

        return cnt%1000000007;;
    }
};
```
1590. 使数组和能被 P 整除

题意

求删除一个子数组后，余下数组和能整除 p。

分析

假设 sum 为整个数组的和，m 为删除子数组的和。

那么要求即使得 (sum-m)%p=0。因为都是正数，根据同余定理，则 sum%p=m%p.

sum 和 p 都是已知的，问题在于 m 怎么求，也就是求一个子数组的和。显然使用前缀和来做比较好。构造前缀和数组 presum。

则 m=presum2-presum1.故 (presum2-presum1)%p=sum%p. 而 sum 和 p 都是已知的，假设值为 k，故即使得 (presum2-presum1)%p=k.

则 presum2-presum1=np+k，presum2=presum1+np+k,presum2%p=(presum1+np+k)%p=(presum1+k)%p.

所以，有 presum2%p=(presum1+k)%p 满足，其中 k=sum%p.

即对于 presum2，有 presum1 满足上面这个公式，显然这是一个存在性问题，所以，用哈希表存 (presum1+k)%p，然后遍历 presum2，看 presum2%p 是否存在于哈希表中，如果存在，则满足条件，然后更新长度即可。

最后注意长度不能为 nums.size()，即不能删除所有元素，和 sum<p 可以提前剪枝，或·sum%p==0 也直接满足等其它条件了。

代码
```
class Solution {
public:
    int minSubarray(vector<int>& nums, int p) {
        long long sum=0;
        int k;
        for (int i=0;i<nums.size();i++){
            sum+=nums[i];
        }
        if (sum<p){
            return -1;
        }
        k=sum%p;
        if (k==0){
            return 0;
        }

        vector<long long> presum(nums.size()+1);
        int min=99999999;
        unordered_map<int,int> m;

        m[k%p]=0;
        for (int i=1;i<presum.size();i++){
            presum[i]=presum[i-1]+nums[i-1];
            if (m.count(presum[i]%p)>0){
                min=min<(i-m[presum[i]%p])?min:(i-m[presum[i]%p]);
            }
            m[(presum[i]+k)%p]=i;
        }
        
        if (min==99999999 || min==nums.size()){
            return -1;
        }

        return min;
    }
};
```

差分数组

list

1893. 检查是否区域内所有整数都被覆盖

题意分析

这个题给一些 ranges 区间，然后又给一个 [l,r] 区间，要求 [l,r] 区间中的每个数都至少在 ranges 区间里出现一次

暴力思考

我们先来暴力分析，既然 [l,r] 中的每个数都需要判断，那么我们就遍历这些数即可。问题在于怎么判断一个数是否在 ranges 区间中出现。

再暴力自然是遍历 ranges 区间，然后依次判断该数是否在区间中，如果全都不在则不符合。

显然我们需要同时遍历两个区间，时间复杂度自然是 $O (n^{2})$ 。

优化思考

上面我们判断每个数是否出现在区间中时，遍历了 ranges 数组，其实没有必要这么做。既然已经提前给定了 ranges 数组，那么我们可不可以提前把它们合并成一个区间，然后 key 为数字，value 为是否在区间中呢？类似进行 hash 的处理，之后我们判断数是否存在时，直接判断 value 即可。

如 ranges=[[1，4]，[3，5]]，l = 2，r=5

对于 ranges，我们先给定一个比较大的区间

无效的图片地址

有

无效的图片地址

在窗口中的说明存在，变成 1

无效的图片地址

如果得到了这个数组，那么要判断某个数是否存在就很简单了，直接判断 value 是否为 1 即可。假设已经预处理了该数组，那么遍历 [l,r] 的时间复杂度就变成了 $O (n)$ .

但是现在还有一个问题，那就是我们怎么根据 ranges 区间集合，生成上面那个预处理的数组。

我们再来看图

无效的图片地址

要生成目标数组，显然我们只需要把窗口中的数批量增加 1 即可。而这，典型的对数组进行批量修改，所以我们可以用差分数组的思想来做。

比如说我们要把 [1,4] 区间加一

无效的图片地址

我们只需要 presum[1]++,presum[4+1]— 即可。

无效的图片地址

同理另一个区间

无效的图片地址

然后我们由差分数组生成原数组，需要计算每个数的前缀和。

无效的图片地址

我们会发现，其实这个数组就是各个数字的出现次数

无效的图片地址

看上去似乎和我们之前想要的 value 都是 1 有点区别，其实是一样的，都是 1 表示的是是否存在，而这里只要大于 1 就表示存在了。

显然上面我们只遍历了一次 ranges ，故时间复杂度是 $O (n)$ .总的时间复杂度也是 $O (n) .$

对了，还有差分数组设置为多大的问题，由于给定 ranges 数字最大为 50，而 50 为右区间时，进行操作是 50+1 索引，故设置 52 大即可。

代码

class Solution {
public:
    bool isCovered(vector<vector<int>>& ranges, int left, int right) {
        vector<int> diffsum(52);

				// 修改差分数组
        for (auto i : ranges){
            diffsum[i[0]]++;
            diffsum[i[1]+1]--;
        }

				// 前缀和处理得到原数组
        for (int i=1;i<diffsum.size();i++){
            diffsum[i]+=diffsum[i-1];
        }

				// 判断
        for (int i=left;i<=right;i++){
            if (diffsum[i]==0){
                return false;
            }
        }
        return true;
    }
};

1109. 航班预订统计

题意

对区间批量修改，求最终的区间

分析

区间的批量修改问题，典型的使用差分数组使用。

优化

null

效率

时间复杂度： $O (n)$

空间复杂度： $O (n)$

代码

class Solution {
public:
    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        vector<int> res(n);

        for (vector<int>& b : bookings) {
            res[b[0]-1]+=b[2];
            if (b[1] < n) {
                res[b[1]]-=b[2];
            }
        }

        for (int i=1;i<n;i++){
            res[i]+=res[i-1];
        }

        return res;
    }
};

1094. 拼车

题意

对区间批量增加元素，求原数组是否有元素大于 capacity.

分析

由于车站有上车有下车，比较麻烦，故我们可以先假设车的容量有无限大，可以一直上车，然后最后我们再看过程中是否有某个站超过了容量。

那么，就是一个典型的对某区间进行批量修改，最后求原数组的过程，故使用差分数组。

优化

null

效率

时间复杂度： $O (n)$

空间复杂度： $O (n)$

代码

class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        vector<int> diffsum(1000);

        for (vector<int> &t : trips){
            diffsum[t[1]]+=t[0];
            if (t[2]+1<1000) {
                diffsum[t[2]]-=t[0];
            }
        }

        for (int i=1;i<1000;i++){
            if (diffsum[i-1]>capacity){
                return false;
            }
            diffsum[i]+=diffsum[i-1];
        }

        return true;
    }
};

56. 合并区间

题意

合并重叠区间

分析

把所有区间映射到一个数组中，然后遍历该数组，连续的就是应该合并的。

优化

效率

代码

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {        
        vector<vector<int>> res;
        vector<int> diff(10002);
        int a,b;
        vector<int> t;
        sort(intervals.begin(),intervals.end());

        for (vector<int>& i:intervals){
            diff[i[0]]++;
            diff[i[1]+1]--;
        }
        
        if (diff[0]!=0){
            t.push_back(0);
        }

        for (int i=1;i<10002;i++){
            diff[i]+=diff[i-1];
            if ((diff[i-1]==0) && (diff[i]!=0)){
                t.push_back(i);
            }
            if ((diff[i-1]!=0) && (diff[i]==0)){                
                t.push_back(i-1);
            }
            if (t.size()==2){
                res.push_back(t);
                t.clear();
            }
        }

        return res;
    }
};

面试题 16.10. 生存人数

题意

求区间批量查询后的数组最大值

分析

总数组 0~100 年（1900 偏移），对于每个人，都在其中一个区间活着，故设原数组每个值存活着的人，那么对于每个人，显然需要在他活着的那段区间加一，最后再求总数组的最大值。

显然，这是一个典型的数组的批量区间修改，故使用差分数组。

优化

无

代码

class Solution {
public:
    int maxAliveYear(vector<int>& birth, vector<int>& death) {
        int res;
        int year=1900;
        vector<int> diffsum(102);

        for (int i=0;i<birth.size();i++){
            diffsum[birth[i]-1900]++;
            diffsum[death[i]+1-1900]--;
        }

        res=diffsum[0];

        for (int i=1;i<102;i++){
            diffsum[i]+=diffsum[i-1];
            if (res<diffsum[i]){
                res=diffsum[i];
                year=1900+i;
            }
        }

        return year;
    }
};

1854. 人口最多的年份

题意

求区间批量查询后的数组最大值

分析

总数组 0~100 年（1950 偏移），对于每个人，都在其中一个区间活着，故设原数组每个值存活着的人，那么对于每个人，显然需要在他活着的那段区间加一，最后再求总数组的最大值。

优化

null

效率

时间复杂度： $O (n)$

空间复杂度： $O (n)$

代码

class Solution {
public:
    int maximumPopulation(vector<vector<int>>& logs) {
        int res;
        int year=1950;
        vector<int> diffsum(102);

        for (vector<int>& i: logs) {
            diffsum[i[0]-1950]++;
            diffsum[i[1]-1950]--;
        }

        res=diffsum[0];

        for (int i=1;i<102;i++){
            diffsum[i]+=diffsum[i-1];
            if (res<diffsum[i]){
                res=diffsum[i];
                year=1950+i;
            }
        }

        return year;
    }
};

二维前缀

二维使用容斥定理构造前缀和，只是构造比较简单，背个模板即可。而对所有子矩阵遍历是 $O (n^{4})$ 的时间复杂度，比较高，所以常见的优化是使用哈希表，先固定上下边，然后固定左边或右边，就能通过根据三边确定矩阵，降到 $O (n^{3})$ .

list

304. 二维区域和检索 - 矩阵不可变

题意

这个题给一个矩阵，然后求任意子矩阵的和。

一维前缀和

在一维数组中，如果我们要求子数组的和，我们通常是这么做的：

无效的图片地址

我们把所有点到原点的和先计算出来，然后要求区间 sub 时，只需两个和相减即可。

$s u b = s_{1} - s_{2}$ .

假设用 presum 表示该数组，那么 presum[i] 就表示 nums[i] 前所有数之和，注意不包括 nums[i].

并且为了方便编程，我们通常会增加一个元素，使得 presum[0] 的 0，即第一个元素的前缀和等于 0，当然实际上前面并没有元素，当时如果不这么做，假设我们要求 [0,r] 区间的解，就需要判断 l 是否等于 0，然后结果为 presum[r].当时我们引入 0 后，就变成 presum[r]-presum[0] 和普通的 [l,r] 相同，这大大的方便了我们的编写。

二维引入

我们知道，在一维中引入前缀和数组大大的提高了查询区间和的效率，同样的，在二维矩阵中，我们也可以使用类似的思想提高效率。

在一维中，我们把区间和变成了两个前缀和之差，在二维中，我们则可以把待求矩阵变成一些面积运算的结果

无效的图片地址

如上图，显然待求面积 $S_{4} = S - S_{1} - S_{2} + S_{3}$ .

对于一维数组中，前缀和 presum[i] 表示点 i 到原点的距离，而在二维，我们可以类似的，用 presum[i][j] 表示点 (i,j) 到原点 (0,0) 的面积。

无效的图片地址

presum 矩阵就是每个点到原点面积组成的矩阵。

不过同样的为了编程，如遇到 (0,0) 到原点组成的矩阵面积，如果 presum[i][j] 点 (i,j) 的话，显然 presum[i][j] 就等于 nums[i][j]，但是若我们遇到 i 或 j 为 0 时，我们就需要判断

进行处理。

所以我们将 presum 矩阵增加一行一列，presum[i][j] 表示 0~~i-1,0~~j-1 组成的矩阵，而不包括 (i,j) 所在的行列。

无效的图片地址

例子

上面光看分析有些枯燥，我们来看个例子。

现给原矩阵如下

无效的图片地址

那么前缀和矩阵为

无效的图片地址

如 presum[4][3]=26

无效的图片地址

就表示 0~~3 行，0~~2 列组成的矩阵和

无效的图片地址

显然 3+1+5+6+3+1+2+4+1=26.

生成 presum

我们接着来看怎么生成 presum 矩阵

无效的图片地址

显然对于任意一个点 (i,j)，它的面积应该等于 $p res u m [i] [j] = p res u m [i] [j - 1] + p res u m [i - 1] [j] - p res u m [i - 1] [j - 1] + m [i - 1] [j - 1]$ .

如 $p res u m [4] [3] = p res u m [4] [2] + p res u m [3] [3] - p res u m [3] [2] + n u m s [3] [2] = 22 + 21 - 17 + 0 = 26$ .

无效的图片地址

即

3 0 1          3 0       3 0 1      3 0     
5 6 3          5 6       5 6 3      5 6
1 2 0     =    1 2   +   1 2 0   -  1 2    +
4 1 0          4 1                               1

注意 presum 最左边和最上侧都是 0，故 presum 应该从 presum[1][1] 开始计算。

求解子矩阵和

现在我们知道了 presum 的含义和求法，又知道子矩阵应该表示为几个前缀和的运算，我们来看一下具体应该怎么转换。

对于点 (r1,c1),(r2,c2) 组成的矩阵，由于 presum 不包含点的行列，故要包含该点所在的行列的话，需要都加一，故 r1++,c1++,r2++,c2++.

并有图得

无效的图片地址

故 $s = p res u m [ro w 2] [co l 2] - p res u m [ro w 2] [co l 1 - 1] - p res u m [ro w 1 - 1] [co l 2] + p res u m [ro w 1 - 1] [co l 1 - 1]$

代码

class NumMatrix {
private:
    vector<vector<int>> presum;

public:
    NumMatrix(vector<vector<int>>& matrix) {
        presum.resize(matrix.size()+1,vector<int>(matrix[0].size()+1));
        for (int i=1;i<=matrix.size();i++){
            for (int j=1;j<=matrix[0].size();j++){
                presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+matrix[i-1][j-1];
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        row1++;
        col1++;
        row2++;
        col2++;

        return presum[row2][col2]-presum[row2][col1-1]-presum[row1-1][col2]+presum[row1-1][col1-1];
    }
};

1314. 矩阵区域和

题意

求任意区域和

分析

对于点 (i,j)，显然就是求 (i-k,j-k) 到 (i+k,j+k) 区域的和。而这是典型的未修改数组的区间查询操作，故建立二维前缀和，具体可参考 304.

然后需要注意的是 (i-k,j-k) 可能下溢，所以要和 0 比较下，而 (i+k,j+k) 可能上溢，所以要和 presum.size()-1 比较下。

效率

时间复杂度：建立前缀和 O(n^2)，查询 O(1).

空间复杂度：O(n^2).

代码

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& matrix, int k) {
        vector<vector<int>> presum;        
        presum.resize(matrix.size()+1,vector<int>(matrix[0].size()+1));
        vector<vector<int>> res;
        res.resize(matrix.size(),vector<int>(matrix[0].size()));
        int row1;
        int col1;
        int row2;        
        int col2;        

        for (int i=1;i<=matrix.size();i++){
            for (int j=1;j<=matrix[0].size();j++){
                presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+matrix[i-1][j-1];
            }
        }

        for (int i=0;i<matrix.size();i++){
            for (int j=0;j<matrix[0].size();j++){
                row1=max(0,i-k);
                col1=max(0,j-k);
                row2=min(i+k+1,(int)(presum.size()-1));
                col2=min(j+k+1,(int)(presum[0].size()-1));

                res[i][j]=presum[row2][col2]-presum[row2][col1]-presum[row1][col2]+presum[row1][col1];
            }
        }

        return res;
    }
};

1074. 元素和为目标值的子矩阵数量

题意

求子矩阵和为 target 的数目

分析

构造前缀和，然后暴力查询，优化个锤子。

优化

效率

时间复杂度：构造 O(mn)，查询 O(mmn*n).

空间复杂度：O(mn).

代码

class Solution {
public:
    int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
        int cnt=0;     
        long presum [matrix.size()+1][matrix[0].size()+1];      
        
        for (int i=1;i<=matrix.size();i++){
            for (int j=1;j<=matrix[0].size();j++){
                presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+matrix[i-1][j-1];
            }
        }

        for (int i=0;i<matrix.size();i++){
            for (int j=0;j<matrix[0].size();j++){
                for (int m=i;m<matrix.size();m++){
                    for (int n=j;n<matrix[0].size();n++){
                        if ((presum[m+1][n+1]-presum[m+1][j]-presum[i][n+1]+presum[i][j])==target){
                            cnt++;
                        }
                    }
                }
            }
        }

        return cnt;
    }
};

363. 矩形区域不超过 K 的最大数值和

题意

求子矩阵和≤k的最大值

分析

构造前缀和，然后暴力查询，优化个锤子。

优化

效率

时间复杂度：构造 O(mn)，查询 O(mmn*n).

空间复杂度：O(mn).

代码

class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        long presum [matrix.size()+1][matrix[0].size()+1];
        int res=-99999;
        
        for (int i=1;i<=matrix.size();i++){
            for (int j=1;j<=matrix[0].size();j++){
                presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+matrix[i-1][j-1];
            }
        }

        for (int i=0;i<matrix.size();i++){
            for (int j=0;j<matrix[0].size();j++){
                for (int m=i;m<matrix.size();m++){
                    for (int n=j;n<matrix[0].size();n++){
                        int t=presum[m+1][n+1]-presum[m+1][j]-presum[i][n+1]+presum[i][j];                        
                        if (t==k) {
                            return t;
                        } else if (t<k){
                            res=max(t,res);
                        }
                    }
                }
            }
        }
        return res;
    }
};

面试题 17.24. 最大子矩阵

题意

求最大子矩阵和

分析

构造前缀和，然后暴力查询，优化个锤子。

优化

效率

时间复杂度：构造 O(mn)，查询 O(mmn*n).

空间复杂度：O(mn).

代码

暴力

class Solution {
public:
    vector<int> getMaxMatrix(vector<vector<int>>& matrix) {
        vector<int> res;
        int sum=-9999999;       
        long presum [matrix.size()+1][matrix[0].size()+1];
        int row1, col1, row2, col2;
        
        for (int i=1;i<=matrix.size();i++){
            for (int j=1;j<=matrix[0].size();j++){
                presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+matrix[i-1][j-1];
            }
        }

        for (int i=0;i<matrix.size();i++){
            for (int j=0;j<matrix[0].size();j++){
                for (int m=i;m<matrix.size();m++){
                    for (int n=j;n<matrix[0].size();n++){
                        int t=presum[m+1][n+1]-presum[m+1][j]-presum[i][n+1]+presum[i][j];       
                        if (t>sum) {
                            sum=t;
                            row1=i;
                            col1=j;
                            row2=m;
                            col2=n;
                        }
                    }
                }
            }
        }

        res.push_back(row1);
        res.push_back(col1);
        res.push_back(row2);
        res.push_back(col2);
    
        return res;
    }
};

1292. 元素和小于等于阈值的正方形的最大边长

题意

求子方阵和≤k 的最大边长

分析

涉及到未修改数组的区间和查询，典型引入前缀和优化，故构造前缀和。

子矩阵由于是个方阵，故不能通过枚举左上顶点和右下顶点确定区域，只需枚举左上顶点 (i,j) 和边长 k 即可，那么右下顶点自然就是 (i+k,j+k).

那直接枚举左上顶点和边长暴力查询和即可。

优化

像上面那样枚举的复杂度有些高，其实这题还有一些优化的点：

由于要求最大边长，那么没必要每次都从 0 开始枚举边长，直接从当前求出的最大边长枚举即可。
由于矩阵的元素都大于等于 0，那么左上顶点不变时，随着边长的增加，那么数组和一定也是增加的，那么，如果当前的和已经大于了阈值 threshold ，说明后面更大的矩阵也是大于的，而我们要求小于等于的矩阵，所以后面的矩阵直接剪枝即可。

效率

优化前后的复杂度相同

时间复杂度：建立 $O (m * n)$ ，查询 $O (m * n * min (mn))$

空间复杂度： $O (m * n)$ .

代码

暴力

class Solution {
public:
    int maxSideLength(vector<vector<int>>& matrix, int threshold) {
        int res=0;
        vector<vector<int>> presum;
        presum.resize(matrix.size()+1,vector<int>(matrix[0].size()+1));        
        for (int i=1;i<=matrix.size();i++){
            for (int j=1;j<=matrix[0].size();j++){
                presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+matrix[i-1][j-1];
            }
        }

        for (int i=0;i<matrix.size();i++){
            for (int j=0;j<matrix[0].size();j++){
                for (int k=0;(k+i<matrix.size()) && (k+j<matrix[0].size());k++){
                    long long sum=presum[i+k+1][j+k+1]-presum[i+k+1][j]-presum[i][j+k+1]+presum[i][j];
                    if (sum<=threshold) {
                        res=max(res,k+1);
                    }
                }
            }
        }

        return res;
    }
};

优化

class Solution {
public:
    int maxSideLength(vector<vector<int>>& matrix, int threshold) {
        int res=0;
        vector<vector<int>> presum;
        presum.resize(matrix.size()+1,vector<int>(matrix[0].size()+1));        
        for (int i=1;i<=matrix.size();i++){
            for (int j=1;j<=matrix[0].size();j++){
                presum[i][j]=presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+matrix[i-1][j-1];
            }
        }

        for (int i=0;i<matrix.size();i++){
            for (int j=0;j<matrix[0].size();j++){
								// 优化1：k=res;
                for (int k=res;(k+i<matrix.size()) && (k+j<matrix[0].size());k++){
                    long long sum=presum[i+k+1][j+k+1]-presum[i+k+1][j]-presum[i][j+k+1]+presum[i][j];
                    if (sum<=threshold) {
                        res=max(res,k+1);
                    } else {
                        break; // 优化2：break;
                    }
                }
            }
        }

        return res;
    }
};

1738. 找出第 K 大的异或坐标值

题意

求二维前缀异或 top k 问题

分析

涉及未修改数组的批量区间查询，典型使用前缀和的场景，不过运算由加法变成了异或，由于加法和整数能构建为群，所以和加法的使用方式类似。

构建前缀和时，和加法有一些区别：

无效的图片地址

我们知道二维前缀和基于容斥定理，即先求并集，再求交集，即

$p res u m [i] [j] = p res u m [i - 1] [j] + p res u m [i] [j - 1] - p res u m [i - 1] [j - 1] + m [i - 1] [j - 1]$ .

但是异或稍微有些不同，我们知道 $x \oplus x = 0, 0 \oplus x = x$ .

故 $p res u m [i - 1] [j] \oplus p res u m [i] [j - 1]$ 将重复的部分消去了，故应该在异或起来，即

$p res u m [i - 1] [j] \oplus p res u m [i] [j - 1] \oplus p res u m [i - 1] [j - 1]$ ，还有一个点，即 $m [i - 1] [j - 1]$ .同样异或起来，故最终：

$p res u m [i] [j] = p res u m [i - 1] [j] \oplus p res u m [i] [j - 1] \oplus p res u m [i - 1] [j - 1] \oplus m [i - 1] [j - 1] .$

前缀异或数组构建好了之后，要求的就是在数组中找到第 k 大的元素，这就是一个 topk 的问题，只不过变成二维数组了而已，可以用快速选择，堆等方法来做，这里使用了堆。只需直接放到大顶堆中，然后弹出 k-1 个元素即可，余下堆顶的元素就是要求的。

效率

时间复杂度： $O (m * n * l o g^{mn})$ ，遍历元素 $O (mn)$ ，建堆 $O (l o g^{m} n)$

空间复杂度： $O (mn)$

代码

class Solution {
public:
    int kthLargestValue(vector<vector<int>>& matrix, int k) {
        int res=0;
        priority_queue<int> heap;
        vector<vector<int>> presum;
        presum.resize(matrix.size()+1,vector<int>(matrix[0].size()+1));        
        for (int i=1;i<=matrix.size();i++){
            for (int j=1;j<=matrix[0].size();j++){
                presum[i][j]=presum[i-1][j]^presum[i][j-1]^presum[i-1][j-1]^matrix[i-1][j-1];
                heap.push(presum[i][j]);
            }
        }

        for (int i=0;i<k-1;i++){
            heap.pop();
        }

        return heap.top();
    }
};

位运算+dp+状态压缩+前缀和

list

1915. 最美子字符串的数目

1371. 每个元音包含偶数次的最长子字符串

1177. 构建回文串检测

1542. 找出最长的超赞子字符串

广义前缀

广义前缀是指类似于前缀和，同样使用前缀避免重复运算，常见的有前缀异或，前缀积等。

list

1352. 最后 K 个数的乘积

题意

求最后 k 个数的积

分析

最暴力的显然是直接开个数组，每次遍历后 k 个即可，不过会超时。而且由于数组的个数在变化，因此比较麻烦。

优化

求数组相邻元素的积，显然和前缀和思想类似，所以我们来考虑一下。而且由于是后 k 个数的积，那么考虑后缀积如何。

如果数组没有变化的话，是可以的，但是由于数组在变化，因此后缀积是不行的，因为每次后缀都在变化，要使用后缀积的话，所有积都得变。

那么只能考虑前缀积了，要求区间积就只能两区间相除。但是有一个问题，那就是如果积为 0 的话，显然是不能除的。

而且数组增加元素只是后缀变了，而前缀积都是相同的。故每次增加元素，只需增加新的一个前缀积即可。即新元素乘以前一个前缀积。

所以增加元素时要分两种情况：
1. 当 num ≠0 时，直接新元素 num * 前一个前缀积即可。
2. 当 num = 0 时，当前前缀积理论上为 0，但是，如果这样插入进去的话，那么后面的前缀积都会为 0，求区间积时就会出错。而实际上，当新元素为 0 时，以后的所有元素的后缀积都会为 0，所以我们没必要再弄什么前缀积，直接返回 0 即可。而再增加元素则要重新计算。如 [1,2,0] 的后缀积都为 0，但是增加 [1,2,0,1] 的后缀积就有一个 1 了，和去掉 0 前元素的前缀积计算方式相同，即 [1] 的前缀积。
同理，获取后缀积时，也要分两种情况：
1. 前面说了，当新增元素为 0 时，前缀积要清空，新的前缀积没有 0，而超出这个长度的后缀积都为 0
2. 普通情况直接总积/前缀积即可。
显然获取和增加元素的时间复杂度都是 O(1),而空间复杂度是 O(n).

代码

暴力
```
class ProductOfNumbers {
private:
vector<int> presum;

public:
    ProductOfNumbers() {        
    }
    
    void add(int num) {
        presum.push_back(num);
    }
    
    int getProduct(int k) {        
        int res=1;
        for (int i=0;i<k;i++){
            res*=presum[presum.size()-1-i];
        }
        return res;
    }
};
```
优化
```
class ProductOfNumbers {
private:
vector<int> persum;

public:
    ProductOfNumbers() {
        persum=vector<int>(1,1);
    }
    
    void add(int num) {
        if (num==0){
            persum=vector<int>(1,1);
        } else {
            persum.push_back(persum.back()*num);
        }
    }
    
    int getProduct(int k) {
        if (persum.size()<=k){
            return 0;
        }
        return persum.back()/persum[persum.size()-k-1];
    }
};
```
238. 除自身以外数组的乘积

题意

求除了当前元素构成的乘积数组

分析

最自然的想法，自然是总乘积/当前元素，这样 O(n) 就能实现，但是题目要求不能用除法，而且元素为 0 也很特殊，所以得优化下。

优化

求乘积子数组比较少见，不过求和倒是很常见，假设这题求的是除了当前元素的和，又该怎么求呢？

涉及未修改区间的批量查询，所以引入前缀和，但是问题在于，除了当前元素=当前元素前面的元素+后面的元素。光是前缀和怎么能求呢。

既然这样，那就类似的再引入一个后缀和即可，当前元素的和就等于前缀和+后缀和，所以提前构建两个数组，再遍历一遍原数组，共时间复杂度还是 O(n)，不过空间复杂度变成了 O(n).

其实还可以进行一下优化，我们没必要把前缀和后缀和数组真的求出来，直接在结果数组上存储即可。先求前缀和，然后后缀和的每个元素在加上对于的前缀和，就直接求出来结果，但是减少了一次遍历和存储空间。

至于这题是乘积，直接把加法变成乘法即可。

代码
```
class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        vector<int> res;
        vector<int> l(nums.size());
        vector<int> r(nums.size());
        l.insert(l.begin(),1);
        r.insert(r.end(),1);

        for (int i=1;i<l.size();i++){
            l[i]=l[i-1]*nums[i-1];
        }

        for (int i=r.size()-2;i>=0;i--){
            r[i]=r[i+1]*nums[i];
        }

        for (int i=0;i<nums.size();i++){
            res.push_back(l[i]*r[i+1]);
        }

        return res;
    }
};
```
```
class Solution {
public:
    vector<int> constructArr(vector<int>& nums) {
        vector<int> res(nums.size());
        if (nums.empty()){
            return res;
        }        
        int tmp=1;
        res[0]=1;
        for (int i=1;i<nums.size();i++){
            tmp*=nums[i-1];
            res[i]=tmp;
        }
        tmp=1;
        for (int i=nums.size()-2;i>=0;i--){
            tmp*=nums[i+1];
            res[i]*=tmp;
        }
        return res;
    }
};
```
1310. 子数组异或查询

题意

求任意区间的异或结果

分析

数组未修改，又求任意数组的性质，显然满足前缀和的使用性质，故引入前缀和，只是运算变成异或。

引入前缀异或 $p res u m [i] = a [0] \oplus a [1] \oplus ... \oplus a [i - 1]$

则当 j≥i 时， $p res u m [j + 1] = a [0] \oplus a [1] \oplus a [i - 1] \oplus a [i] \oplus ... \oplus a [j] = p rs u m [i] \oplus a [i] \oplus ... \oplus a [j]$

则区间 [i,j] 的异或值 $a [i] \oplus ... \oplus a [j] = p res u m [j + 1] \oplus p res u m [i]$ .

故只需建立前缀异或数组，然后对相应的两个值异或即可。

代码
```
class Solution {
public:
    vector<int> xorQueries(vector<int>& arr, vector<vector<int>>& queries) {
        vector<int> res;
        arr.insert(arr.begin(),0);
        for (int i=1;i<arr.size();i++){            
            arr[i]^=arr[i-1];
        }

        for (int i=0;i<queries.size();i++){
            res.push_back(arr[queries[i][1]+1]^arr[queries[i][0]]);
        }
    
        return res;
    }
};
```
1442. 形成两个异或相等数组的三元组数目

题意

求两个区间异或和相等

分析

已知：

$0 <= i < j <= k < a rr . l e n g t h a = a rr [i] \oplus a rr [i + 1] \oplus ... \oplus a rr [j - 1] b = a rr [j] \oplus a rr [j + 1] \oplus ... \oplus a rr [k]$

分析题目给定的提交，发现和前缀和的格式非常相似，所以我们考虑引入前缀异或

$p res u m [i] = a rr [0] \oplus a rr [1] \oplus a rr [2] ... \oplus a rr [i - 1]$

即 presum[i] 等于前 i 个数的异或值

同理，有

$p res u m [j] = a rr [0] \oplus a rr [1] \oplus ... \oplus a rr [i - 1] \oplus a rr [i] \oplus .. \oplus a rr [j - 1] = p res u m [i] \oplus a rr [i] \oplus ... \oplus a rr [j - 1] a = a rr [i] \oplus ... \oplus a rr [j - 1] = p res u m [i] \oplus p res u m [j]$

$p res u m [k + 1] = a rr [0] \oplus a rr [1] \oplus ... \oplus a rr [i] \oplus .. a rr [j - 1] \oplus a rr [j] \oplus ... \oplus a rr [k] = p res u m [i] \oplus a rr [i] \oplus a rr [k] = p res u m [j] \oplus a rr [j] \oplus ... \oplus a rr [k] b = a rr [j] \oplus ... \oplus a rr [k] = p res u m [j] \oplus p res u m [k + 1]$

故要使得 a=b，即 $p res u m [i] \oplus p res u m [j] = p res u m [j] \oplus p res u m [k + 1]$ ，即 $p res u m [i] = p res u m [k + 1]$ .

这就转换为常见的前缀和题型了，简单的直接暴力遍历两次 $O (n^{2})$ 即可。

需要注意的是，虽然给你 i,j,k 三个数，但是使 a=b 根本和 j 无关，故当 i，k 确定后，i 和 k 之间有多少元素，就有多少个（i,j,k) 个满足条件。即 k-i 个。

优化

像 presum[i]=presum[k+1] 这种存在性问题，常见的可直接用哈希表优化到线性去，这题同样的，我们考虑优化。

假设 arr = [2,3,1,6,7] ，则 presum[0,2,1,0,6,1]，满足条件的显然有 [0,2,1,0]，[1,0,6,1]，而两个区间中都分别有两个元素，故共 4 个。

问题在于，[0,2,1,0] 这种区间怎么求，显然这种区间的条件是左右端点相等，且长度大于等于 3.

我们假设当前遍历右端点为 k,那么要找到左端点 i，假设满足条件的有 i1,i2,i3..

那么结果 cnt=(k-i1)+(k-i2)+..(k-in)=nk-(i1+i2+i3+..in)

换句话说，当右端点固定后，要找到以当前点为右端点中满足的区间个数，需要知道和右端点值相等的左端点的个数 n 和所有下标的值。

那么我们可以用两个哈希表，以 presum[i] 为 key，一个 value 为个数 n，一个为和 sum，然后计算，再把当前点记录到哈希表中，最后遍历结束即可。

显然时间和空间复杂度都是 O(n).

代码

暴力
```
class Solution {
public:
    int countTriplets(vector<int>& arr) {
        int res=0;
        arr.insert(arr.begin(),0);

        for (int i=1;i<arr.size();i++){
            arr[i]^=arr[i-1];
        }

        for (int i=0;i<arr.size();i++){
            for (int k=i+1;k<arr.size()-1;k++){
                if (arr[k+1]==arr[i]){
                    res+=k-i;
                }
            }
        }

        return res;
    }
};
```
优化
```
class Solution {
public:
    int countTriplets(vector<int>& arr) {
        int res=0;
        unordered_map<int,int> cnt,sum;
        arr.insert(arr.begin(),0);
        
        cnt[0]++;
        sum[0]=0;
        for (int i=1;i<arr.size();i++){
            arr[i]^=arr[i-1];
            if (cnt.count(arr[i])>0){
                res+=(i-1)*cnt[arr[i]]-sum[arr[i]];
            }            
            cnt[arr[i]]++;
            sum[arr[i]]+=i;
        }

        return res;
    }
};
```
1829. 每个查询的最大异或值

题意

求一个数，使得数组异或结果为最大值。

分析

题目没有说清楚，maximumBit 是个什么东西，其实就是最大值的位数，既然如此，那么最大值其实就是 2**maximumBit-1.

也就是说，求一个数 k，使得 k^sum=2maximumBit-1，那么自然 k=sum ^ 2maximumBit-1.

而 sum 就是每个元素的前缀异或，不过是从右往左而已，既然如此，那就构造前缀异或，然后从右遍历，再和最大值异或就是结果了。

效率

时间复杂度 O(n)，空间复杂度 O(n).

代码
```
class Solution {
public:
    vector<int> getMaximumXor(vector<int>& nums, int maximumBit) {
        vector<int>res;
        int max=pow(2,maximumBit)-1;
        for (int i=1;i<nums.size();i++){
            nums[i]^=nums[i-1];
        }
        for (int i=nums.size()-1;i>=0;i--){
            res.push_back(max^nums[i]);
        }
        return res;
    }
};
```

后缀数组和

后缀数组和 suffix 和前缀和 prefix 类似，不过是从后缀开始求和。

同时后缀和与前缀和有时经常同时使用，方式都是确定数组上一点为分割点，然后两边分别记录一个值。

比如 1477 和 926，都是找到一个分割点，然后左边数组的 x 和右边数组 y 的什么东西，建立前后缀数组 prefix [i] 和 suffix [i]，prefix [i] 就表示分割点 i 左边的什么，suffix [i] 就表示分割点右边的什么，然后遍历分割点 i，就同时综合左右两边找到最优解。

1477 是 i 左右两边和为 target 的最短长度，而 926 则 prefix [i] 是分割点 i 左边 1 的个数，suffix [i] 是分割点 j 右边 0 的个数，然后扫描 i 求和的最小值即可。

list

1477. 找两个和为目标值且不重叠的子数组

题意

求不重叠且和均为 target 的两数组的长度的最小值

分析

这题涉及批量求数组和，那么就可以想到可能要用到前缀和数组。如果只是求和为 target 的数组的话，是很好求的，就是第 560 题。

但是这题要两数组不重叠，该怎么做呢？

我们可以确定一个点，数组分别在这个点左右，那么两数组就一定不重叠。我们遍历这个交界点，那么就能确定所有分割的情况。

现在假设我们确定了这个点，现在要求什么？两数组的和等于 target。所以我们分别在两边找到和等于 target 的数组，然后呢？

又要两数组长度最短，所以我们在左边和为 target 的数组里找到最短长度，右边也找到最短长度，然后和就是当前分割点的最短长度了。

最后在遍历分割点，找到所有分割点下的最短长度的最小值。

思路很清晰了，现在问题就有：如何找到分割点两侧和为 target 的最短长度？简化一下，就是如何找到何为 target 的最短长度？再简化一下，就是如何找到和为 target 的数组？

最后一个简化的问题就是 560 题了，我们需要建立该前缀和数组，然后我们扫描固定数组右端点，然后用哈希表找到该值，哈希表存的是左侧 key=nums[i]+target，value 的坐标，如果 nums[i] 在哈希表里，说明左边存在点 nums[j]+target=nums[i]，即 sum=nums[i]-nums[j]=target 数组和为 target 了，然后更新长度即可。

同理，右侧数组也是一样的。

我们每确定一个分割点之后，都要像上面这样找到两侧的最短长度，难道每次都要这么去扫描一遍吗？

其实没有必要，因为它们的计算过程都是类似的，那么我们提前把这些值求出来即可。

所以我们提前开两个数组 prefix 和 suffix，prefix[i] 存点 i 左边数组中，和为 target 的最短长度，suffix[i] 存点 i 右边数组中，和为 target 的最短长度，然后对于分割点 i，要求的总最短长度就等于 prefix[i]+suffix[i].

优化

do nothing.

效率

时间复杂度： $O (n)$

空间复杂度： $O (n)$

代码

class Solution {
public:
    int minSumOfLengths(vector<int>& arr, int target) {
        int t=0;
        int size=0;
        int res=arr.size()+1;
        vector<int> prefix(arr.size()+1);
        vector<int> suffix(arr.size()+1);
        vector<int> prefixSum(arr.size()+1);
        vector<int> suffixSum(arr.size()+1);

        unordered_map<int,int> mp;
        unordered_map<int,int> ms;

  			// 左侧
        mp[target]=0;
        for (int i=1;i<prefixSum.size();i++){
            prefixSum[i]=prefixSum[i-1]+arr[i-1];
            t=prefix[i-1];
            if (mp.count(prefixSum[i])>0){
                if (t==0){
                    t=i-mp[prefixSum[i]];
                } else {
                    t=min(t,i-mp[prefixSum[i]]);
                }                
            }
            prefix[i]=t;
            mp[target+prefixSum[i]]=i;
        }

				// 右侧
        ms[target]=0;
        for (int i=suffixSum.size()-1;i>0;i--){
            size=suffixSum.size()-i;        
            suffixSum[size]=suffixSum[size-1]+arr[i-1];            
            t=suffix[size-1];
            if (ms.count(suffixSum[size])>0){
                if (t==0){
                    t=size-ms[suffixSum[size]];
                } else {
                    t=min(t,size-ms[suffixSum[size]]);
                }                               
            }
            suffix[size]=t;
            ms[target+suffixSum[size]]=size;            
        }

				// 扫描分割点
        for (int i=1;i<suffix.size();i++){
            if (prefix[i]!=0 && suffix[arr.size()-i]!=0){                
                res=min(res,prefix[i]+suffix[arr.size()-i]);
            }
        }

        return res==(arr.size()+1)?-1:res;
    }
};

926. 将字符串翻转到单调递增

题意

将 0 1 相互转换后变成递增的形式，求最小转换次数

分析

类似于 1477，这个题也是可以找到一个分割点，将其分成两个数组，本题分割点左边的数组最后要变成 0，故需要找到所有 1，右边则要变成 1，故要找到 0.

也就是说，假设分割点为 i，那么 i 左边 1 的个数加上 i 右边 0 的个数就是最后要替换的次数，而要求的就是这个次数的最小值，那么，我们就可以枚举所有分割点，然后找到替换次数的最大值。

对于 i 左边的数组，显然就是求 i 左边 1 的个数，就等于左边所有元素之后，即前缀和，所以左边数组可以维护一个前缀和数组。prefix[i] = k 就表示 i 左边 1 的个数为 k。

同理，对于 i 右边的数组，要求 0 的个数，我们可以把 0 和 1 交换一下数字，那么右边 0 的个数也等于右边元素的和，即后缀和，故 suffix[i]=m 就表示 i 右边 0 的个数为 m。

而要求 max(k+m)，则遍历一遍 i，求 max(prefix[i]+suffix[i]) 即可。

优化

do nothing.

效率

时间复杂度： $O (n)$

空间复杂度： $O (n)$

代码

class Solution {
public:
    int minFlipsMonoIncr(string s) {
        int res=s.size();
        vector<int> prefix(s.size()+3);
        vector<int> suffix(s.size()+2);

        for (int i=1;i<=s.size();i++){
            prefix[i]=prefix[i-1]+s[i-1]-'0';
            suffix[s.size()-i+1]=suffix[s.size()-i+2]+'1'-s[s.size()-i];
        }

        for (int i=0;i<=s.size();i++){
            res=min(res,prefix[i]+suffix[i+1]);
        }

        return res;
    }
};

238. 除自身以外数组的乘积

题意

求除了当前元素构成的乘积数组

分析

最自然的想法，自然是总乘积/当前元素，这样 O(n) 就能实现，但是题目要求不能用除法，而且元素为 0 也很特殊，所以得优化下。

优化

求乘积子数组比较少见，不过求和倒是很常见，假设这题求的是除了当前元素的和，又该怎么求呢？

涉及未修改区间的批量查询，所以引入前缀和，但是问题在于，除了当前元素=当前元素前面的元素+后面的元素。光是前缀和怎么能求呢。

既然这样，那就类似的再引入一个后缀和即可，当前元素的和就等于前缀和+后缀和，所以提前构建两个数组，再遍历一遍原数组，共时间复杂度还是 O(n)，不过空间复杂度变成了 O(n).

其实还可以进行一下优化，我们没必要把前缀和后缀和数组真的求出来，直接在结果数组上存储即可。先求前缀和，然后后缀和的每个元素在加上对于的前缀和，就直接求出来结果，但是减少了一次遍历和存储空间。

至于这题是乘积，直接把加法变成乘法即可。

代码

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        vector<int> res;
        vector<int> l(nums.size());
        vector<int> r(nums.size());
        l.insert(l.begin(),1);
        r.insert(r.end(),1);

        for (int i=1;i<l.size();i++){
            l[i]=l[i-1]*nums[i-1];
        }

        for (int i=r.size()-2;i>=0;i--){
            r[i]=r[i+1]*nums[i];
        }

        for (int i=0;i<nums.size();i++){
            res.push_back(l[i]*r[i+1]);
        }

        return res;
    }
};

class Solution {
public:
    vector<int> constructArr(vector<int>& nums) {
        vector<int> res(nums.size());
        if (nums.empty()){
            return res;
        }        
        int tmp=1;
        res[0]=1;
        for (int i=1;i<nums.size();i++){
            tmp*=nums[i-1];
            res[i]=tmp;
        }
        tmp=1;
        for (int i=nums.size()-2;i>=0;i--){
            tmp*=nums[i+1];
            res[i]*=tmp;
        }
        return res;
    }
};

1525. 字符串的好分割数目

题意

求左右两边数组字符种类相等的个数

分析

和 926，1477 差不多，找分割点，然后两边分别构建前后缀数组，再遍历一遍即可，区别只是数组的内容不同而已。

这题确定分割点后，然后需要直到两边数组的字符种类，而这些可以提前构建好，prefix[i] 表示 i 左边数组的字符种类，suffix[i] 表示右边的，构建好了后判断是否相等即可。然后遍历分割点即可。

优化

无

效率

时间复杂度： $O (n)$

空间复杂度： $O (n)$

代码

class Solution {
public:
    int numSplits(string s) {
        vector<int> prefix(s.size()+1);
        vector<int> diffix(s.size()+1);
        unordered_map<int,int> mp;
        unordered_map<int,int> dp;
        int t=0;
        int res=0;

        for (int i=1;i<s.size();i++){            
            t=s.size()-i;
            prefix[i]=prefix[i-1]+1-mp.count(s[i-1]);
            diffix[t]=diffix[t+1]+1-dp.count(s[t]);
            mp[s[i-1]]++;
            dp[s[t]]++;
        }

        for (int i=1;i<s.size();i++){      
            res+=(prefix[i]==diffix[i]);
        }

        return res;
    }
};

其它

其它题型

list

862. 和至少为 K 的最短子数组

题意

找到和大于等于k的子数组

分析

涉及未修改数组的区间查询，显然可以用前缀和。故构造前缀和数组 presum。

要求 sum=presum2-presum1≥k，最简单的直接遍历两次 presum 即可，时间复杂度为 $O (n)$ .

优化

本题数量级在 10^5，暴力显然会超时，考虑优化。

要求 sum=presum2-presum1≥k → presum1≤presum2-k.

遍历 presum2，以它为区间右端点，那么左端点 presum1 需要满足 ≤presum2-k 这个条件，显然这是一个范围值，而不是一个确定的存在性问题，所以显然不能像常见的前缀和优化一样，使用哈希表。

那么这个题应该怎么做呢？

当 presum2 固定后，presum1≤presum2-k，presum2-k 是确定的值，而 presum1 可能有很多满足的值。而本题还要求区间最短，那么显然应该选择 presum1 中满足条件中，最右边的那个，即假设 presum1 索引为 i，那么 i 最大的那个。

但是，我们怎么知道哪些 presum1 满足条件呢？固定 presum2 后，然后又遍历寻找 presum1 吗？但是这样显然就和暴力一样了。

显然我们需要找一个数据结构来维护 presum1，避免暴力穷举。我们来看这个数据结构应该满足什么条件：
1. 由于 presum2 一直右移，那么 presum1 也是一直右移，而且不会回溯，那么每次 presum[i] 显然就是一个先进先出的结构
2. 由于要满足 presum1≤presum2-k，显然涉及到大小关系，我们要找到索引 i 最大的那个
即要满足先进先出的结构，又要维护大小关系，显然，我们应该使用单调队列。

队列中的元素显然是 presum2 左边遍历过的元素，并且要维护大小关系，那么应该递增还是递减呢？队列中应该存什么东西呢？

我们要寻找索引 i 最大的那个，自然应该存索引，又要寻找最大的那个，索引应该从一定满足条件到可能不满足条件开始找。而 presum1≤presum2-k，显然当 presum1 越小，越可能满足条件。

所以：
1. 队列中存 presum1 的索引
2. 队列从队首到队尾递增
现在问题就只剩一个，怎么维护这个队列：

怎么出队：

队首出队，显然，我们要找的是满足 presum1≤presum2-k 中索引最大的。所以，应该一直出队，每次出队都满足 ≤ presum2-k，直到不满足未知，最后那个 i 就是要求的索引。

怎么入队：

和普通单调队列一样，如果当前队尾元素比当前元素小，则出队，然后再入队

现在还有两个疑问，就是出队和入队过程中，我们都去掉了一些元素，这些元素不会影响最终结果吗？

先说出队时：

假设当前区间为 [i,j]，j 固定，i 一直在增加，假设 i+3 是最后的结果，问的是 i,i+1,i+2 这几个元素会不会影响。结论是不会，因为我们求的是满足区间的最小长度，那么 [i+3,j] 显然是区间最小的，[i+1,j] 这些满足与否不重要。

再说入队时：

在出队后，队列中所有元素都是 presum1>presum2-k，若队列的元素 presum1>presum2，显然更不可能满足 presum1 ≤ presum2-k，所以需要将它们弹出。

代码

暴力
```
class Solution {
public:
    int shortestSubarray(vector<int>& nums, int k) {
        int min=9999999;
        nums.insert(nums.begin(),0);

        for (int i=1;i<nums.size();i++){
            nums[i]+=nums[i-1];         
        }

        for (int i=0;i<nums.size();i++){
            for (int j=i;j<nums.size();j++){
                if (nums[j]-nums[i]>=k) {
                    min=min<(j-i)?min:(j-i);
                }
            }
        }

        return min==9999999?-1:min;
    }
};
```
优化
```
class Solution {
public:
    int shortestSubarray(vector<int>& nums, int k) {
        int min=9999999;
        int j=0;
        bool f=false;
        vector<long long> presum(nums.size()+1);
        deque<int> q;

        q.push_back(0);
        for (int i=1;i<presum.size();i++){
            presum[i]=presum[i-1]+nums[i-1];
            
            while(!q.empty() && (presum[q.front()] <= (presum[i]-k))) {
                j=q.front();
                f=true;
                q.pop_front();
            }

            if (f){
                min=min<(i-j)?min:(i-j);   
            }
            f=false;
            
            while(!q.empty() && presum[q.back()]>presum[i]) {
                q.pop_back();
            }
            q.push_back(i);
        }

        return min==9999999?-1:min;
    }
};
```
209. 长度最小的子数组

同 862

528. 按权重随机选择

题意

实现返回一个数 i，这个数的概率为 nums[i]/sum.

分析

这个算法其实非常简单而又常用，在赌场中，转盘赌就是这个原理，在 os 中，调度算法有一个叫彩票调度的随机化+权重方法，也是这个原理。在分布式负载均衡中，选择目标节点的随机化+权重方法，也是这个原理，深度学习中的遗传算法等等，用处非常之广。

其实非常简单，我们给每个数确定一个范围，然后随机生成一个数，在哪个范围内就是哪个数。

而范围的大小，就是该数的概率，其实就是古典概型中的均匀分布，用长度表示概率。

而要进行变化的话，需要计算这个数前面有多少个数，所以自然的就计算前缀和。

比如 [3,14,1,7]，前缀和数组为 [3,17,18,25]

无效的图片地址

从 1~25 生成一个随机数 x，显然我们需要在 presum 中找到第一个大于 x 的数，假设 x 为 4，第一个大于 4 的数是 17，所以返回 17 的索引 1.

代码
```
class Solution {
private:
vector<int> presum;

public:
    Solution(vector<int>& w) {
        for (int i=1;i<w.size();i++){
            w[i]+=w[i-1];
        }
        presum=w;
    }
    
    int pickIndex() {
        int m = (rand()%presum[presum.size()-1]) + 1;
        int l=0;
        int r=presum.size()-1;
        int mid=l+(r-l)/2;

        while(l<r){
            mid=l+(r-l)/2;

            if (presum[mid] < m) {
                l=mid+1;
            } else {
                r=mid;
            }
        }

        return l;
    }
};
```
1685. 有序数组中差绝对值之和

题意

result[i]=sum(|nums[i]-nums[j]|) ，求 result 数组

分析

涉及到未修改数组的频繁区间查询，故引入前缀和数组 presum。

$res u lt [i] = s u m (∣ n u m s [i] - n u m s [j] ∣) = (n [i] - n [0]) + (n [i] - n [1]) + ... + (n [i] - n [i - 1]) + (n [i] - n [i]) + (n [i + 1] - n [i]) + (n [i + 2] - n [i]) + .. + (n [j] - n [i]) = (2 i - j) n [i] - (n [0] + n [1] + .. + n [i - 1]) + (n [i + 1] + n [i + 2] + .. + n [j]) = (2 i - j) n [i] - p res u m [i] + p res u m [j + 1] - p res u m [i + 1]$

故构造 presum 数组，然后遍历 i 计算即可。

$res u lt [i] = (2 i - j) n [i] - p res u m [i] + p res u m [j + 1] - p res u m [i + 1]$

优化

do nothing.

效率

时间复杂度： $O (n)$

空间复杂度： $O (n)$

代码
```
class Solution {
public:
    vector<int> getSumAbsoluteDifferences(vector<int>& nums) {
        vector<int> presum(nums.size()+1);
        vector<int> res(nums.size());
        int j=nums.size()-1;

        for (int i=1;i<presum.size();i++){
            presum[i]=presum[i-1]+nums[i-1];
        }

        for (int i=0;i<nums.size();i++){
            res[i]=(2*i-j)*nums[i]-presum[i]+presum[j+1]-presum[i+1];
        }

        return res;
    }
};
```

总结

总的来说，前缀和和差分是一个比较典型和常用的算法技巧，使用的场景也比较广，经常和其它知识点结合起来，不过原理还算简单，属于会了就能做的知识点。

参考